Hybrid Numerical Modelling Approaches Employing Fast Integral Methods
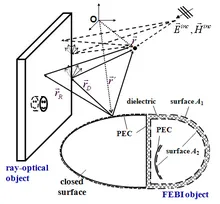
(Α1 and Α2).
Numerical solutions of integral equations (IE) are among the most successful numerical modelling techniques in electromagnetics. Since the field problems are reduced to the determination of equivalent current distributions, very accurate representations of the strongly varying fields close to corners and edges of metallic objects (PEC) are possible and the utilization of Huygens‘ principle makes it possible to design a platform for the combination of various modelling techniques into hybrid methods.
In our research, we investigate hybrid methods combining the finite element (FE) method with boundary integral (BI) methods as well as ray-optical methods utilizing geometrical optics (GO) and the uniform geometrical theory of diffraction (UTD). In order to accelerate the IE solutions, we work with fast integral methods such as the multilevel fast multipole method (MLFMM) or related approaches such as the so-called multilevel fast spectral domain algorithm (MLFSDA), particularly suited for periodic problems. The modelling algorithms are able to process standard mesh formats such as NASTRAN and powerful CAD packages together with their user interfaces can be used to prepare the required meshes.
Our MLFMM implementation works with a particularly efficient representation of the basis function radiation patterns, which has recently even proven to be quite suitable for the treatment of second order basis functions on triangular meshes.
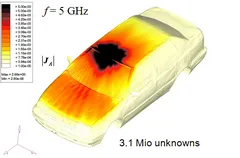
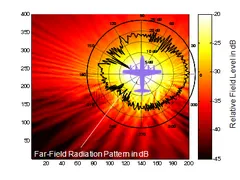
Contact: Prof. Dr.- Ing. Thomas Eibert